CPP-101: Структури

Примери: Точка в равнината

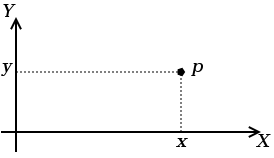
Нека дефинираме структура, която изобразява точка в равнината, като използва нейните декартови координати (вж. фигурата).

Декартови координати на точка в равнината

Структурата може да бъде дефинирана по следния начин:

struct point {
    double x;
    double y;
};

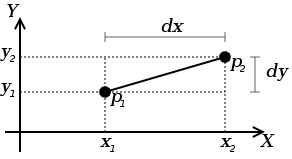
Нека сега дефинираме няколко функции, които използват тази структура. Първата функция, която ще разгледаме е функция, която изчислява разстоянието между две точки в равнината като използва Питагоровата теорема (вж. фигурата).

Разстояние между две точки в равнината

Дефиницията на функцията е представена в следния фрагмент

#include <cmath>
using namespace std;
double distance(point p1, point p2) {
    double dx=p1.x-p2.x;
    double dy=p1.y-p2.y;
    return sqrt(dx*dx+dy*dy);
}

[note]
Сравнете така дефинираната функция distance с дефиницията на същата функция в раздел Дефиниране на функции.
[/note]

Нека разгледаме още две операции, които често се изпълняват върху точки в равнината – операциите събиране и изваждане. Ако имаме две точки [latex]p_1[/latex] и [latex]p_2[/latex] в равнината с декартови координати [latex](x_1, y_1)[/latex] и [latex](x_2, y_2)[/latex] съответно, то сума на точките [latex]p_1+p_2[/latex] се нарича точка от равнината [latex]P=(X,Y)[/latex], чиито координати се изчисляват по следния начин:

[latex]X=x_1+x_2;\ Y=y_1+y_2[/latex].

Функцията, реализираща тази операция, може да се дефинира по следния начин:

point add(point p1, point p2) {
    point result={p1.x+p2.x, p1.y+p2.y};
    return result;
}

Аналогично се дефинира изваждането на точки от равнината. Разликата на две точки в равнината [latex]p_1-p_2[/latex] е отново точка [latex]P=(X,Y)[/latex], чиито координати се изчисляват по следния начин:

[latex]X=x_1-x_2;\ Y=y_1-y_2.[/latex]

Дефиницията на функцията, която реализира операцията изваждане на точки от равнината, е представена в следния фрагмент:

point sub(point p1, point p2) {
    point result={p1.x-p2.x, p1.y-p2.y};
    return result;
}